Détection de fraude bancaire simulée

Novembre 2025

Cette première étape consiste à explorer différents types de graphes afin de mieux comprendre leurs propriétés structurelles.

Méthodologie

J'ai utilisé NetworkX pour générer trois familles de graphes aléatoires :

• Erdős - Rényi : les arêtes sont créées Chaque nœud représente un compte.
• Barabási-Albert : modèle de croissance préférentielle qui produit des réseaux avec des "hubs".
• Watts-Strogatz : réseau petit-monde, qui combine régularité locale et connexions aléatoires.

Pour chaque graphe, j'ai mesuré quelques indicateurs essentiels :

• nombre de nœuds et d'arêtes,
• degré moyen, maximum et minimum,
• centralité (pour identifier les nœuds les plus importants).

Résultat attendu :

Cette exploration permet de comparer différentes topologies de réseaux et de poser les bases nécessaires avant d'introduire la simulation de transactions et de fraude dans les étapes suivantes.

Cette étude illustre comment on peut simuler des transactions bancaires sous forme de graphe et tenter d'y détecter des comportements frauduleux.

A partir d'un réseau artificiel généré avec NetworkX, on applique deux modèles classiques de Machine Learning :

• Régression Logistique (baseline)
• Random Forest

L'objectif est de comprendre leurs performances face à un déséquilibre marqué des classes (fraudes rares).

Pour cette simulation, on génère un graphe de 500 nœuds (représentant des comptes) connectés aléatoirement selon le modèle Erdős-Rényi. Environ 10 % des comptes sont étiquetés comme fraudeurs de manière aléatoire (nœuds rouges). Les nœuds bleus représentent les comptes normaux. Cette visualisation permet de repérer la distribution des fraudes dans le réseau.

Pour chaque nœud, on extrait quatre caractéristiques :

• Degré total
• Degré entrant
• Degré sortant
• Coefficient de clustering

Ces valeurs servent d'entrée aux modèles de Machine Learning, entrainés avec un échantillon équilibré entre comptes normaux et fraudeurs.

Le jeu de données a été séparé en 70 % pour l'entraînement des modèles (train) et 30 % pour l'évaluation (test), en veillant à préserver la proportion des fraudes simulées dans les deux ensembles grâce à un échantillonnage stratifié (stratify=y).

Cette séparation garantit une évaluation fiable des performances des modèles sur des données qu'ils n'ont jamais vues.

Extrait de code :

#  Création du graphe
fraud=0.10
G = nx.erdos_renyi_graph(500, 0.05)
n_frauds = int(n_nodes * fraud)
fraud_nodes = np.random.choice(G.nodes, size=n_frauds, replace=False)

Modèles classiques : Régression Logistique et Random Forest

Afin d'établir une base de comparaison solide , deux modèles classiques ont été testés :

• Régression Logistique, modèle qui sert de 'baseline' simple et interprétable.
• Random Forest, modèle capable de capturer des relations non linéaire entre les caractéristiques.

L'objectif est d'évaluer leur capacité à détecter une faible proportion de transactions frauduleuses dans un grape artificiel généré par NetworkX.

Régression Logistique

• Classe 0 (comptes normaux) : 68 correctement détectés sur 135 $ \rightarrow $ environ 50%
• Classe 1 (fraudes) : 4 correctement détectées sur 15 $ \rightarrow $ seulement 27%.

Comme attendu avec une classe très déséquilibré, le modèle est beaucoup plus performant pour les comptes normaux que pour les fraudes.

Logistic Regression (baseline)
Matrice de confusion :
 [[68 67]
 [11  4]]

                      precision    recall    f1-score    support

           0             0.861       0.504     0.636         135
           1             0.056       0.267     0.093           15

    accuracy                                     0.480         150
   macro avg      0.459     0.385       0.364         150
weighted avg    0.780     0.480       0.581         150

Rapport de classification

• Classe 0 : précision correcte (86 %) mais recall moyen $ \rightarrow $ certains comptes normaux sont mal classés.
• Classe 1 : précision très faible (5.6 %) $ \rightarrow $ la plupart des prédictions de fraude sont incorrectes.
• Le F1-score pour la fraude est très faible (0.093) $ \rightarrow $ cela montre la limite des modèles classiques sur ce type de données déséquilibrées.

La régression logistique appliquée sur le graphe de transactions simulé avec 10 % de fraudes détecte correctement environ la moitié des comptes normaux, mais peine à identifier les fraudes. Le modèle est donc limité par le déséquilibre des classes, ce qui illustre la difficulté des méthodes classiques pour la détection de fraudes rares."

=== Random Forest ===
#  Matrice de confusion
Matrice RF:
 [[134   1]
 [ 15   0]]

Random Forest

La première ligne de la matrice de confusion obtenue avec le modèle Random Forest montre que presque tous les comptes sont correctement classés (134 / 135). La deuxième ligne de la matrice montre qu'il n'y a aucune fraude détectée (0 / 15).

Comme pour la régression logistique, le modèle classique a du mal à détecter les fraudes, surtout avec peu de nœuds frauduleux (10 %).

Rapport RF :
                      precision    recall  bf1-score   support

           0              0.899     0.993      0.944         135
           1              0.000     0.000      0.000           15
    accuracy                                      0.893        150
   macro avg        0.450     0.496      0.472        150
weighted avg      0.809     0.893      0.849        150

• Pour la classe 0 : le recall est excellent (tous les comptes normaux ont quasiment tous été détectés.
• Pour la classe 1 : précision et recall sont égaux à 0 $ \rightarrow $ le modèle ne prédit jamais de fraude.
• Weighted avg / accuracy = 0.893 $ \rightarrow $ la valeur est élevée, mais c'est biaisé par le déséquilibre des classes.

Ce comportement est attendu sur des classes très déséquilibrées (90% normaux / 10% fraude).

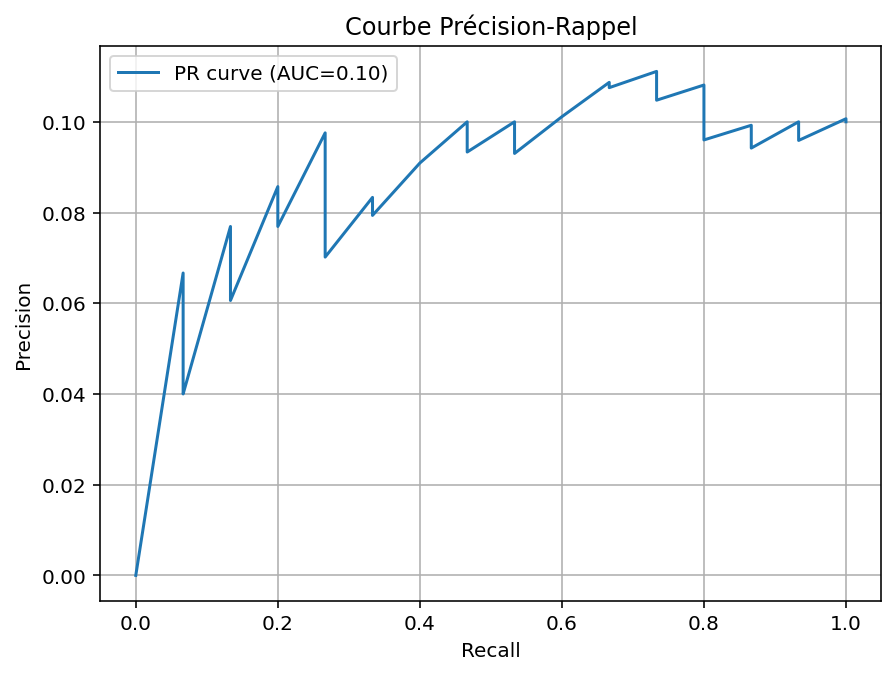
Pour compléter l'évaluation des modèles classiques, on ajoute la courbe Précision-Rappel du Random Forest, particulièrement adaptée aux jeux de données déséquilibrés. Cette courbe montre la performance réelle du modèle pour détecter la fraude, bien plus informative que la simple accuracy.

Approche quantique : classification avec un Quantum SVM (QSVM)

Après avoir testé les modèles classiques (régression logistique et Random Forest), j'ai souhaité explorer une approche plus innovante : un modèle hybride quantique-classique, et plus précisément un Quantum Support Vector Machine (QSVM).

L'objectif est de comparer une méthode traditionnelle avec un modèle quantique afin d'évaluer le potentiel du Quantum Machine Learning dans un contexte de fraude bancaire simulée.

Un QSVM repose sur le même principe qu'un SVM classique : séparer les classes dans un espace de grande dimension grâce à une fonction noyau.

Il y a quand même une différence majeure :

Dans un QSVM, le noyau est calculé par un circuit quantique, ce qui permet d'exploiter un espace de Hilbert potentiellement très complexe, difficile à reproduire classiquement.

Dans le contexte de graphes bancaires :

• chaque nœud (représentant un compte) est représenté par un vecteur de features structurelles : [degré, degré entrant, degré sortant, clustering coefficient],
• ce vecteur est encodé dans l'état d'un circuit quantique,
• ce QSVM apprend la séparation fraude / non fraude dans l'espace quantique.

Résultats QSVM (Quantum Support Vector Machine)

Le Quantum SVM obtient une excellente détection des comptes normaux (99 % de recall) et parvient à mieux distinguer certains cas de fraude que les modèles classiques, avec une précision de 50 % sur la classe fraude (contre 5 à 10 % pour la régression logistique).

Bien que le recall reste faible pour la fraude (7 %), le QSVM montre une véritable capacité à séparer les classes dans un espace de représentation inaccessible aux méthodes classiques. Ce résultat illustre l'intérêt potentiel des kernels quantiques pour la détection d'anomalies rares.

Cette étape illustre comment un modèle quantique peut capturer différemment la structure du graphe, et constitue une première comparaison entre une méthode classique (Logistic Regression, Random Forest) et une approche hybride quantique-classique.

#  Matrice de confusion (QSVM) :
[[134   1]
 [ 14   1]]

• Classe 0 (transactions normales) : 134 correctement classées sur 135 $ \rightarrow $ précision quasi parfaite.
• Classe 1 (fraudes) : 1 détectée sur 15 $ \rightarrow $ faible rappel (6.7 %)
• Contrairement au modèle classique, le QSVM parvient à réduire drastiquement les faux positifs (seulement une erreur sur la classe normale.

=== QSVM (kernel quantique) ===
Classification Report (QSVM) :
              precision          recall    f1-score   support

           0      0.905            0.993     0.947       135
           1      0.500            0.067     0.118        15

    accuracy                                   0.900       150
   macro avg      0.703     0.530     0.532       150
weighted avg    0.865     0.900     0.864       150

• Classe 0 :
  Très bonne précision (0.91), excellent rappel (0.99) $ \rightarrow $ le QSVM classe extrêmement bien les transactions normales.
• Classe 1 (fraude) :
  Précision correcte (0.5), rappel faible (0.07) $ \rightarrow $ Le modèle détecte encore un peu de fraudes, comme les modèles classiques.
• Exactitude globale (accuracy) : 0.90
  Le QSVM égale ou dépasse légèrement les modèles classiques sur l'exactitude globale.

Dans la première partie de mon étude, les modèles supervisés (Régression Logistique, Random Forest et QSVM) ont tous rencontré la même difficulté :

$ \Rightarrow $ Les classes sont extrêmement déséquilibrés (10 % de fraude seulement).

Ce déséquilibre fait que les modèles apprennent très bien à reconnaître les transactions normales, mais pratiquement pas les fraudes, ce qui se traduit par un rappel (recall) très faible pour la classe frauduleuse. Pour améliorer cette situation, j'ai introduit une méthode spécialisée : SMOTE.

Le SMOTE (Synthetic Minority Oversampling Technique) permet de :

• rééquilibrer automatiquement la base d'entraînement en générant artificiellement de nouvelles observations frauduleuses ;
• éviter un surapprentissage trop fort, contrairement à un simple sur-échantillonnage par duplication ;
• améliorer la sensibilité du modèle à la classe minoritaire.

Dans notre cas :

• Avant SMOTE : 35 fraudes uniquement dans le 'train'.
• Après SMOTE : 315 fraudes synthétiques générées $ \rightarrow $ dataset équilibré.

Méthodologie

1. Génération du graphe (Erdős-Rényi, 500 nœuds, 10 % fraude)
2. Extraction de features simples (degree, in-degree, out-degree, clustering)
3. Standardisation des données.
4. Application de SMOTE sur l'ensemble d'entraînement.
5. Entraînement d'une Régression Logistique sur les données équilibrées.
6. Evaluation sur le jeu de test (non modifié).

Résultats obtenus (Logistic Regression + SMOTE)

Matrice de confusion obtenue :

[[75 60]
 [ 7  8]]

Rapport de classification :

• Normal (classe 0)
• précision = 0.915
• recall = 0.556
• 1-score = 0.691
• Fraude (classe 1)
• précision = 0.118
• recall = 0.533
• 1-score = 0.193
• accuracy globale = 0.553

Interprétation

SMOTE change la dynamique du modèle

$ \Rightarrow $ Points positifs

• Le recall sur la fraude augmente fortement : 0.26 $ \rightarrow $ 0.53
  $ \Rightarrow $ Le modèle détecte plus de fraudes qu'avant.
• Le modèle n'ignore plus la classe frauduleuse.

$ \Rightarrow $ Points négatifs

• Le nombre de faux positifs augmente (normal $ \rightarrow $ fraude)
• La précision de la classe fraude reste faible (0.118), ce qui est typique en forte imbalance.

Conclusion

L'usage de SMOTE permet d'obtenir un modèle beaucoup plus sensible aux comportements frauduleux, ce qui est essentiel dans une logique opérationnelle. Même si l'accuracy diminue, la capacité à détecter les fraudes s'améliore réellement, ce qui est l'objectif dans un contexte de risk management.