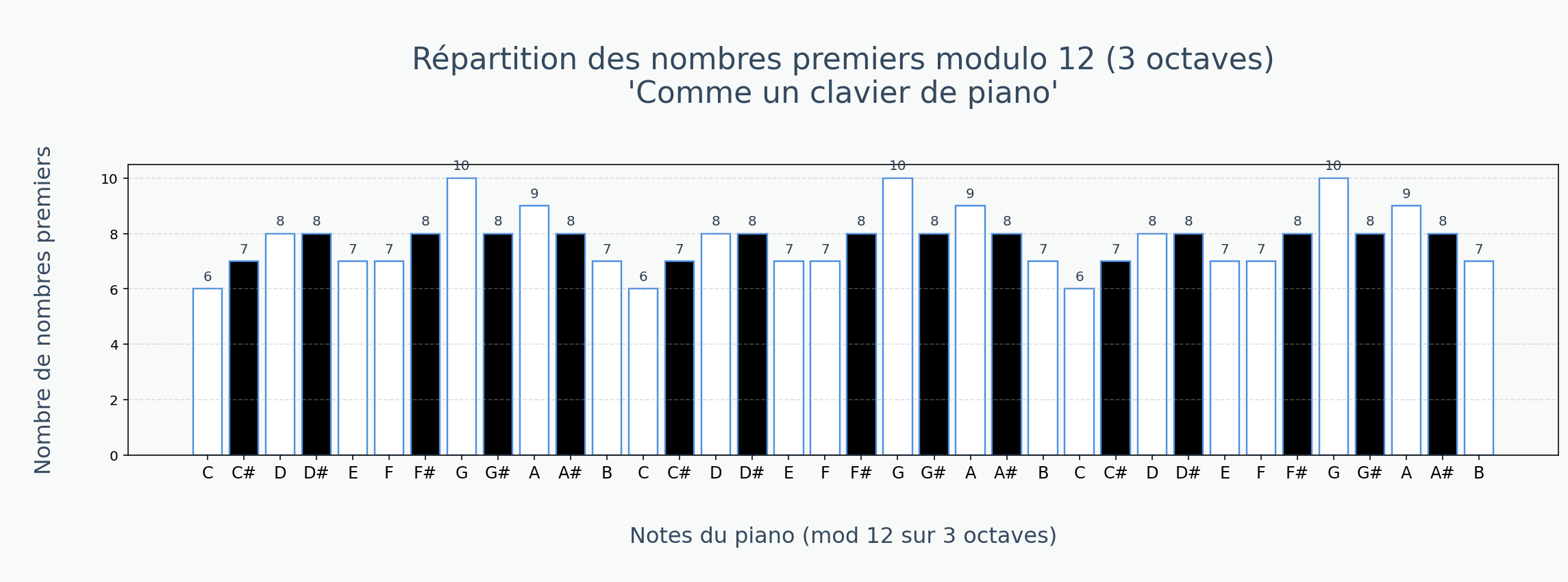
Analyse des fréquences des chiffres dans les 500 premières décimales de π avec Python
Juillet 2025
Dans cette analyse de données avec Python, j'étudie la répartition des chiffres de 0 à 9 dans les 500 premières décimales du nombre π. Après extraction des données et comptage avec des bibliothèques Python comme Pandas et Matplotlib, j'ai visualisé la fréquence d'apparition de chaque chiffre sous forme d'un histogramme.
La majorité des chiffres apparaissent entre 50 et 59 fois, ce qui reflète la répartition pseudo-aléatoire des décimales de π, et tend vers une distribution équilibrée. Cependant, certains chiffres apparaissent moins souvent, ce qui montre que sur 500 décimales, la répartition reste globalement équilibrée mais pas encore parfaitement uniforme.
Cette analyse Python illustre de manière simple la conjecture de normalité de π et montre comment les données peuvent aider à visualiser des concepts mathématiques de façon concrète.
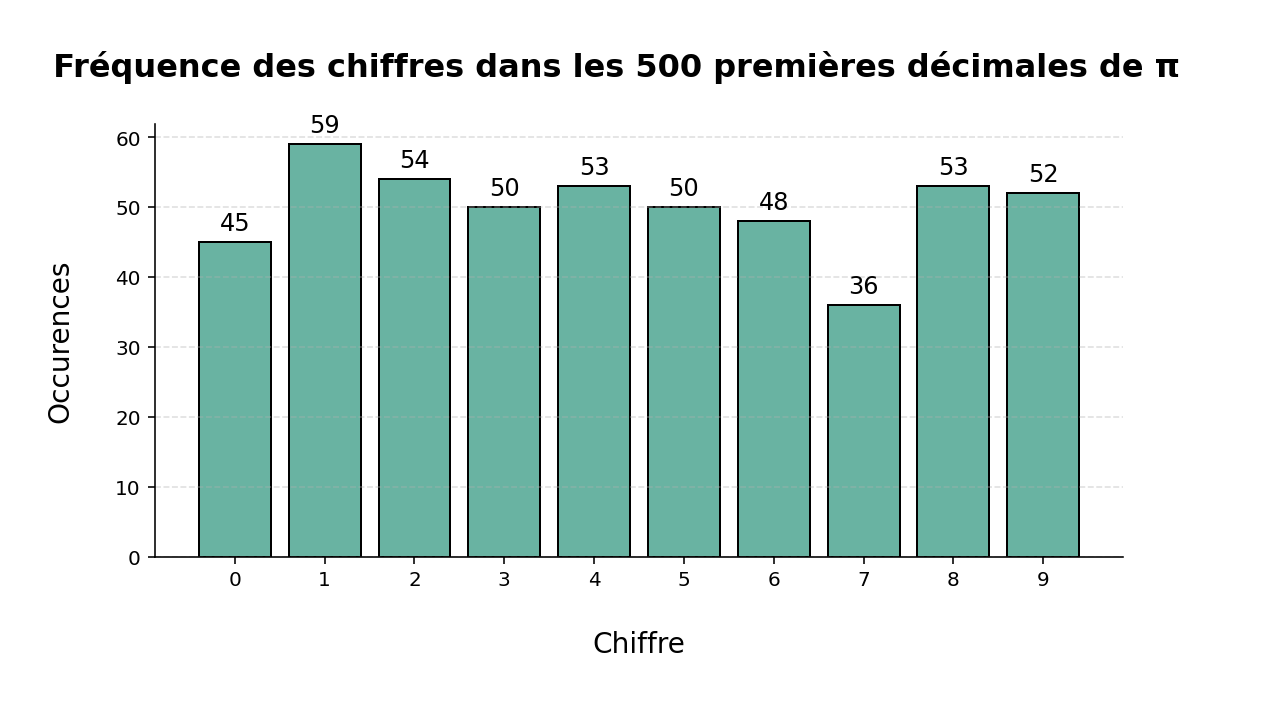
Les nombres premiers se raréfient-ils vraiment ?
Juillet 2025
Dans cette analyse de données avec Python, j'ai étudié la répartition des nombres premiers en traçant le nombre exact de nombres premiers ≤ n et en le comparant à l'approximation de Gauss-Legendre (n/ln(n)).
l'approximation de Gauss suit de près la répartition des nombres premiers jusqu'à environ 50, puis commence à s'en écarter légèrement. Cette divergence montre que les nombres premiers se raréfient de façon irrégulière mais prévisible, confirmant la tendance identifiées par Gauss dès l'âge de 16 ans..
Cette visualisation de données mathématiques illustre comment les outils Python (Pandas, Matplotlib) peuvent être utilisés pour explorer la distribution des nombres premiers et rendre plus accessibles des concepts de théorie des nombres aux passionnés de données.
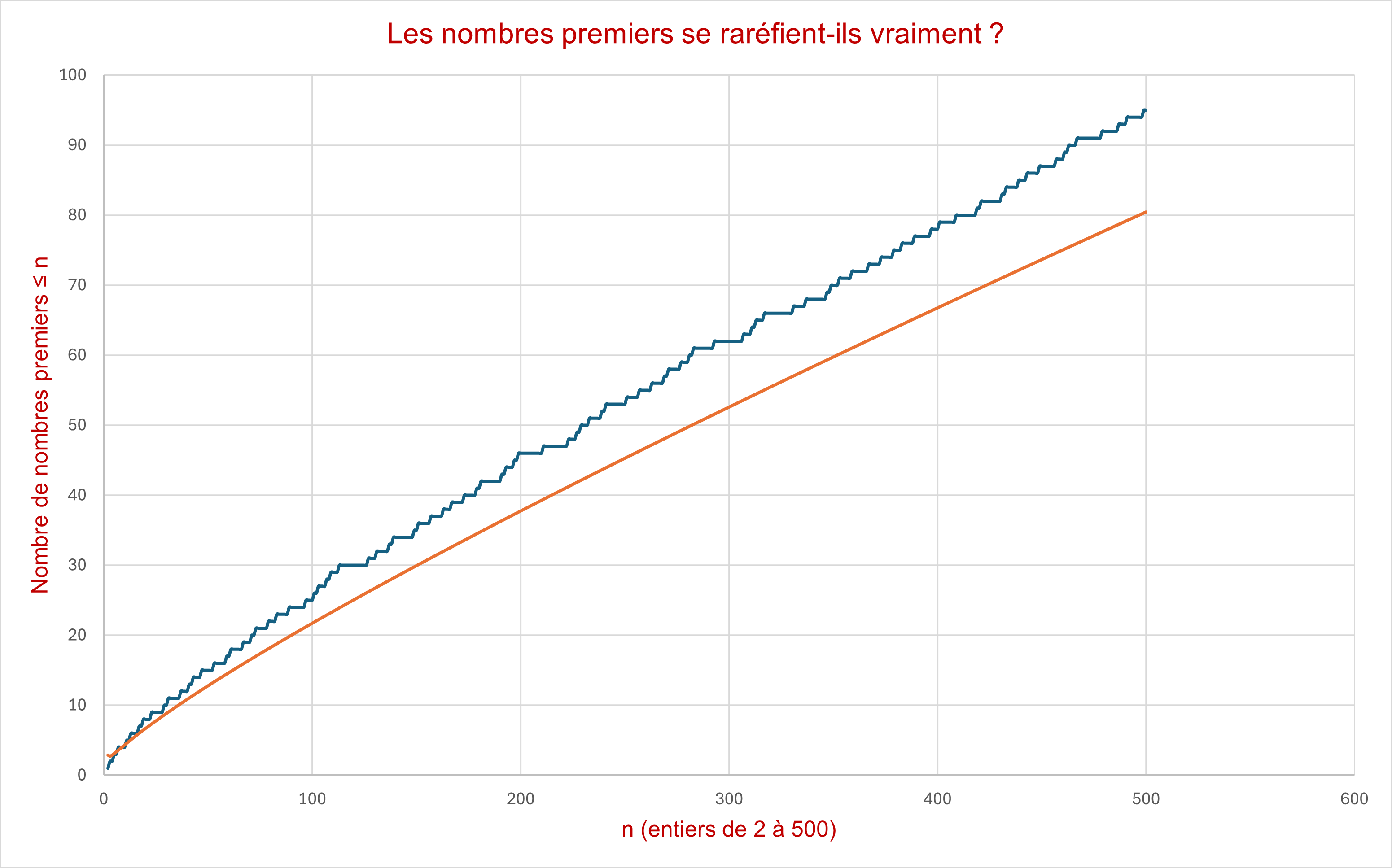
Les nombres premiers jouent-ils du piano ?
Juillet 2025
Dans cette analyse, j'explore la distribution des nombres premiers en les regroupant selon le reste de leur division par 12, comme si l'on répartissait les notes sur un clavier de piano (12 touches par octave).
Chaque barre correspond au nombre de nombres premiers "tombant" sur une note, créant une mélodie visuelle inattendue où certaines notes sont frappées plus souvent que d'autres.
Cette approche permet de visualiser des motifs cachés dans la répartition des nombres premiers, révélant des irrégularités tout en construisant un schéma presque musical.
Voici la correspondance française / anglo-saxonne / nombre mod 12 pour lecture universelle :
Mod 12 Note (FR) Note (EN) 0 DO C 1 DO# C# 2 RE D 3 RE# D# 4 Mi E 5 Fa F 6 Fa# F# 7 Sol G 8 Sol# G# 9 La A 10 La# A# 11 Si B