Exemples avec NetworkX

Article septembre 2025

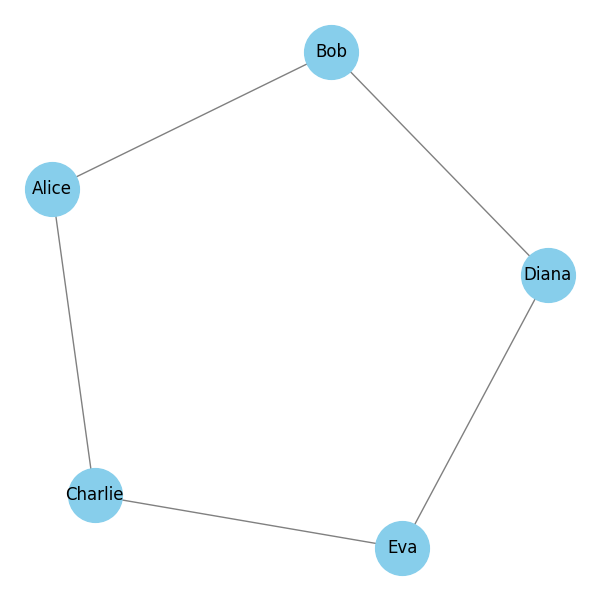
Un réseau (ou graphe) est une manière de représenter des relations entre des entités. Ici, chaque nœud (point) représente une personne, et chaque arête (trait) représente une relation (par exemple, une transaction financière).

Dans ce premier exemple, j'ai créé un mini-réseau fictif avec 5 personnes :

• Alice, Bob, Charlie, Diana et Eva.
• Certaines sont reliées entre elles, ce qui montre qu'il existe une interaction entre elles.

Extrait de code :

# Création d'un petit graphe vide

G = nx.Graph()

# Liste des individus

individuals = ["Alice", "Bob", "Charlie", "Diana", "Eva"]

G.add_nodes_from(individuals)

# Ajout de quelques relations

edges = [("Alice", "Bob"), ("Alice", "Charlie"), ("Bob", "Diana"), ("Charlie", "Eva"), ("Diana", "Eva")]

G.add_edges_from(edges)

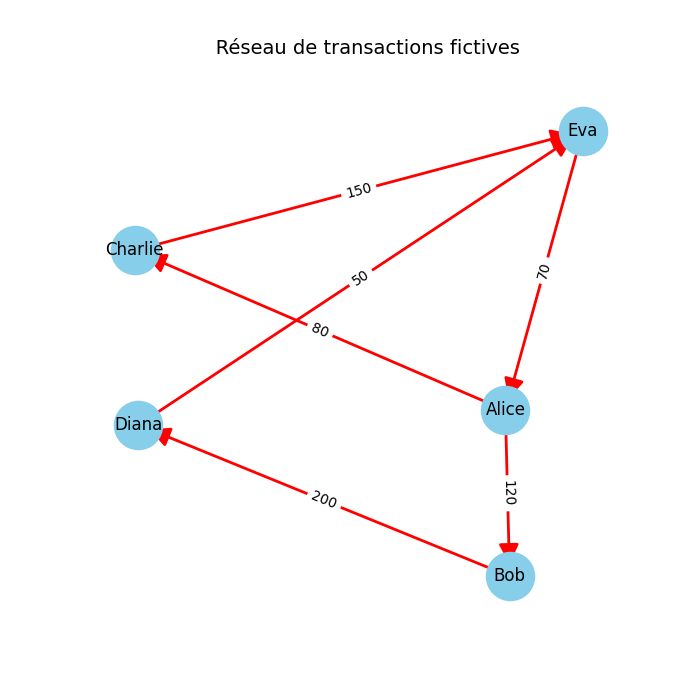
Un graphe peut être enrichi avec des attributs. Dans cet exemple, chaque relation représente une transaction financière : qui a payé qui, et combien. Pour cela :

• Nous utilisons un graphe orienté (les flèches indiquent le sens de la transaction).
• Chaque arête possède un poids (le montant envoyé).
• on affiche les montants directement sur les arêtes.

Le résultat est un réseau de paiements fictifs. Les questions que l'on peut commencer à se poser :

• Qui envoie beaucoup d'argent ?
• Qui reçoit le plus de paiement ?
• Y a-t-il des boucles d'argent (comme Eva qui envoie à Alice). ?

Extrait de code :

# Exemple de transactions fictives (émetteur, receveur, montant)

transactions = [("Alice", "Bob", 120), ("Alice", "Charlie", 80), ("Bob", "Diana", 200), ("Charlie", "Eva", 150), ("Diana", "Eva", 50), ("Eva", "Alice", 70)]

# Ajout des transactions au graphe

for sender, receiver, amount in transactions

G.add_edge(sender, receiver, weight=amount)

Un réseau transactionnel peut cacher des comportements anormaux.

Pour commencer on va appliquer une règle simple :

👉 Lorsqu'un compte envoie plus de 250 unités au total, il est marqué comme suspect.

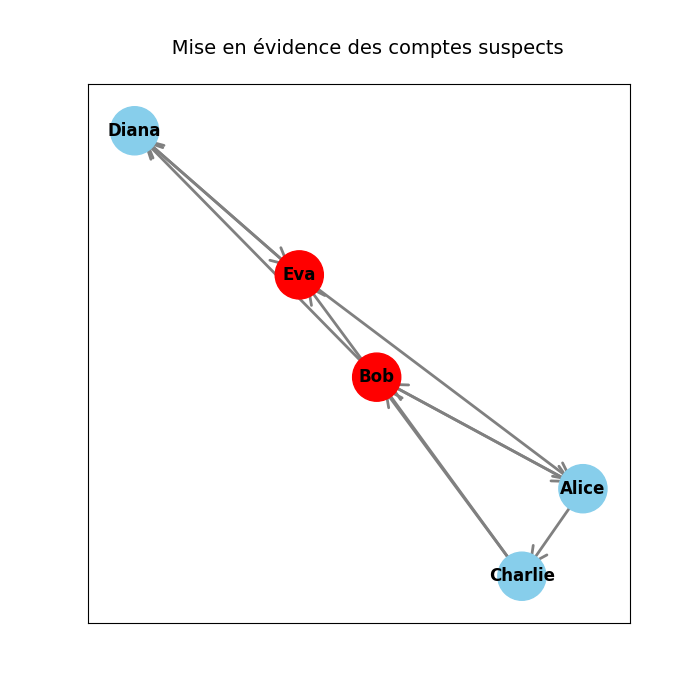
Dans la simulation :

• Chaque nœud représente un compte.
• Chaque lien orienté représente une transaction, avec une flèche du payeur vers le bénéficiaire.
• Les nœuds rouges correspondent aux comptes identifiés comme suspects.

C'est une première approche naïve de détection de fraude :

Elle ne repose pas sur de l'intelligence artificielle mais sur un simple seuil statistique Cependant, elle permet déjà de mettre en évidence certains acteurs centraux du réseau.

Après avoir construit et visualisé le réseau de paiements, nous pouvons maintenant l'analyser à l'aide de métriques de centralité. La centralité permet de mesurer l'importance relative d'un nœud dans un réseau. Dans le cas d'un graphe de transactions financières, un compte qui envoie de l'argent vers de nombreux autres, peut être un signal d'alerte.

Ici, on utilise la centralité de degré sortant (out_degree_centrality).

• Plus un compte envoie de paiements différents, plus sa valeur est élevée.
• Un compte qui redistribue massivement de l'argent peut ainsi être identifié comme potentiellement suspect.

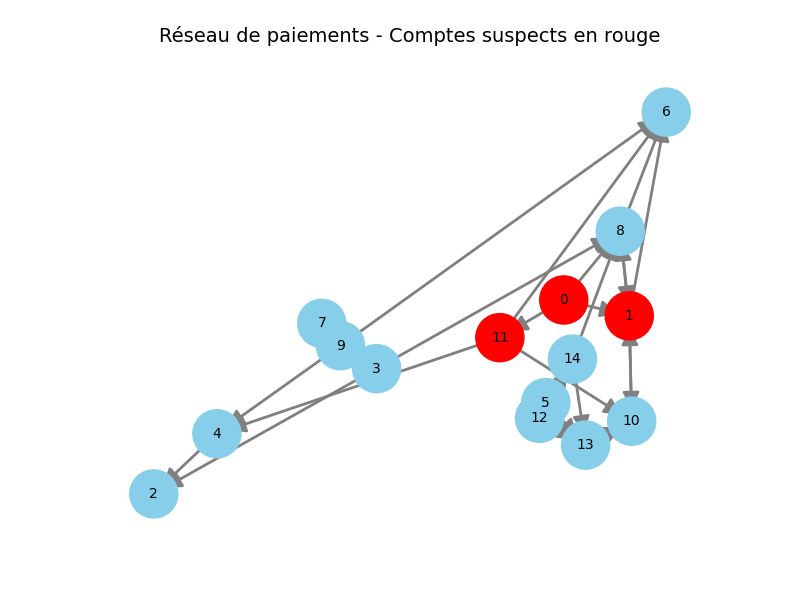
Le graphe ci-dessous illustre ce principe :

• Les nœuds en rouge correspondent aux comptes les plus suspects selon cette métrique.
• Les nœuds en bleu clair représentent les autres comptes.

Cette étape montre comment une simple mesure de centralité peut déjà révéler des structures intéressantes dans un réseau de transaction.

Un cycle correspond à une boucle fermée dans laquelle l'argent part d'un compte, transite par un ou plusieurs autres, puis revient au compte d'origine. Ce type de schéma peut être révélateur de fraudes, comme des transferts circulaires destinés à brouiller les traces ou autre.

Pour identifier ces cycles , nous utilisons la fonction nx.simple_cycles() de la librairie NetworkX. Les nœuds (comptes) impliqués dans au moins un cycle sont colorés en rouge. De plus, toutes les transactions qui participent à un cycle apparaissent en flèches rouges, ce qui rend visible l'ensemble du chemin suspect.

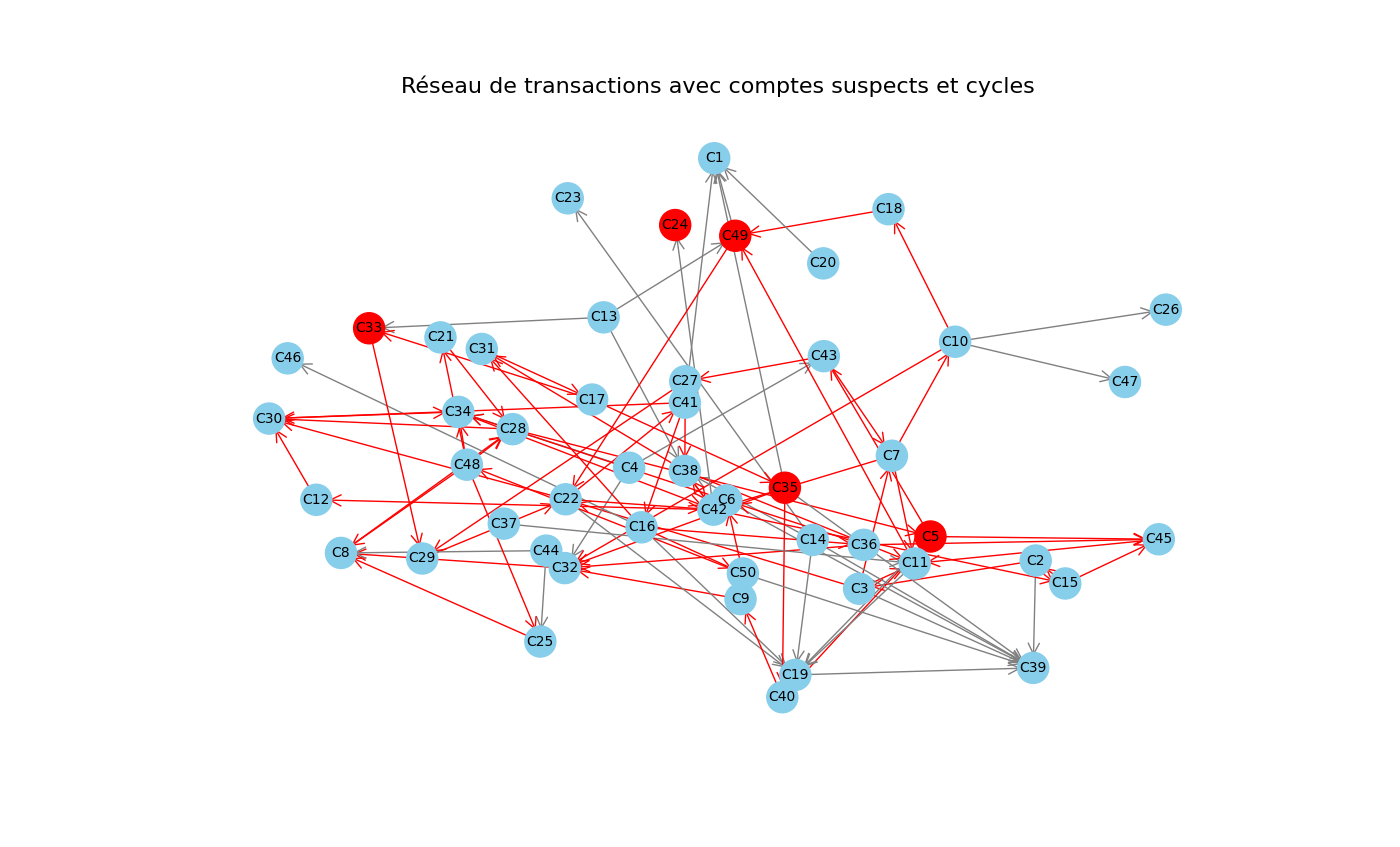
Sur le graphe obtenu, on remarque que :

• Plusieurs comptes apparaissent en rouge : ils sont directement impliqués dans des cycles,
• de nombreuses flèches rouges relient des comptes, mettant en évidence les circuits fermés de transactions.

Cette étape illustre comment une analyse de graphes permet de détecter automatiquement des structures de fraude dans un réseau de paiements.

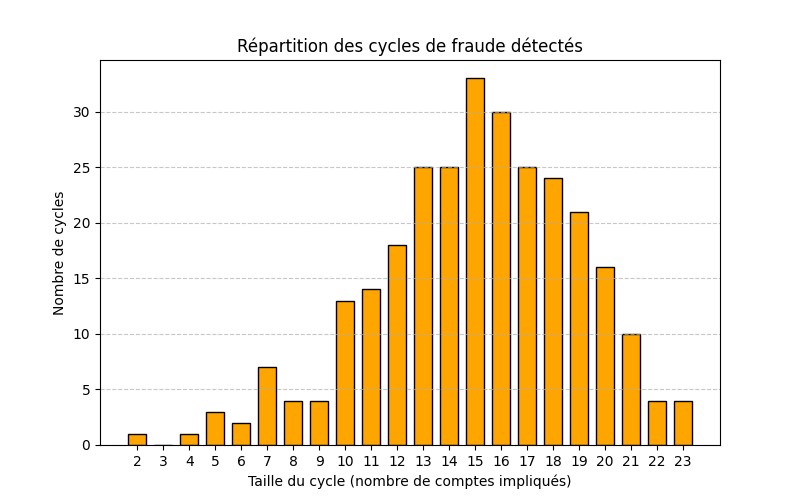
Une fois le réseau construit et les cycles détectés, il est pertinent de visualiser leur répartition selon la taille des boucles. L'histogramme ci-dessous montre le nombre de cycles détectés selon le nombre de comptes impliqués.

L'histogramme met en évidence deux tendances marquées :

1. Cycles courts (2 à 9 comptes), avec 1 à 7 occurrences :

👉 Ce sont des boucles locales, potentiellement des fraudes ponctuelles entre petits groupes ou échanges rapides.

2. Cycles longs (15 à 16 comptes), avec des pics importants (33 et 34 occurrences) :

👉 Ces structures denses suggèrent des mécanismes organisés de transferts circulaires. Dans un contexte réel, ils pourraient indiquer des réseaux complexes de distribution coordonnée ou autre.

En résumé, le réseau révèle une coexistence de schémas isolés et de structures plus massives.. Cette double approche visuelle et statistique contribue à prioriser les enquêtes : les cycles longs sont des signaux forts de fraude organisée, tandis que les cycles courts méritent d'êtres surveillés comme alertes initiales.

Dans cette dernière étape, nous allons plus loin que la simple analyse de réseau . On utilise NetworkX et le Machine Learning afin de simuler un système de détection automatique de fraude.

1. Génération du réseau

On commence à créer un graphe aléatoire dirigé de 50 nœuds avec la fonction nx.erdos_renyi_graph. Chaque nœud représente un compte et chaque arête représente une transaction.

👉 Il s'agit d'une simulation fictive, mais elle reflète la problématique réelle d'un déséquilibre : très peu de fraudeurs au milieu d'une majorité d'utilisateurs normaux.

2. Extraction des caractéristiques

Pour alimenter le modèle, on extrait plusieurs features de graphe pour chaque compte :

• degree : nombre total de connexions (activité générale),
• in_degree : nombre de connexions entrantes (argent reçu),
• out_degree : nombre de connexions sortantes (argent envoyé),
• clustering : tendance du compte à appartenir à un groupe de transactions.

Ces indicateurs permettent de quantifier le comportement d'un compte dans le réseau.

3. Entraînement du modèle

On utilise un classifieur de régression logistique avec l'option class_weight="balanced" afin de corriger le déséquilibre entre fraudeurs et non-fraudeurs. Le modèle est entraîné sur 70% des comptes et testé sur les 30% restants.

👉 Objectif : apprendre à distinguer un comportement frauduleux d'un comportement normal.

4. Évaluation et résultats

On utilise le F1-score comme indicateur principal. Dans nos résultats, nous obtenons un score autour de 0,25.

• Cela montre que le modèle détecte certaines fraudes, mais en manque d'autres.
• Des faux positifs apparaissent aussi (des comptes normaux classés comme suspects).

👉 C'est volontaire : le but est de montrer une situation réaliste. En pratique, les modèles de détection de fraude ont rarement des scores parfaits.

5. Visualisation

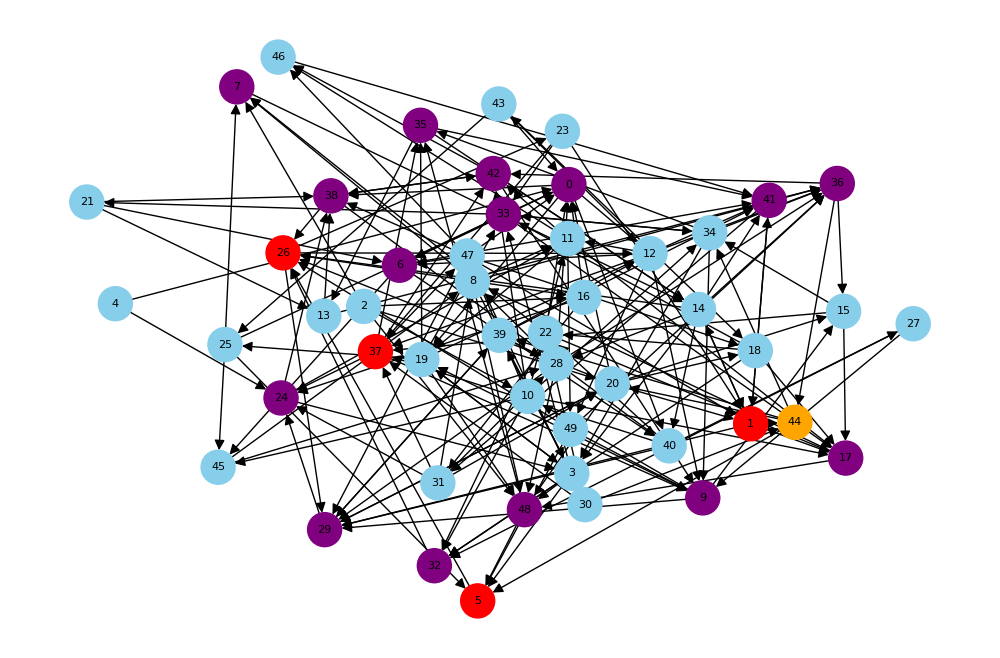
On représente le réseau et on colore les comptes selon la prédiction

• rouge : fraude bien détectée (vraie alerte)
• orange : fraude non détectée (faux négatif)
• violet : compte normal détecté comme fraude
• bleu : compte normal bien classé

Cette visualisation rend immédiatement visible la performance du modèle et illustre les limites d'un système automatique.

Conclusion

Grâce à cette étape, on a pu :

👉 Passer d'une simple exploration de graphe (NetworkX) à une analyse prédictive avec apprentissage automatique, en illustrant de manière pédagogique la détection de fraude et ses difficultés.