⚛️ Python Quantique avec Qiskit

Mise à jour mars 2026

Qu'est-ce qu'un qubit ?

Le qubit est l'unité fondamentale de l'information quantique.
Contrairement à un bit classique, il peut être dans une combinaison des états \( |0\rangle \) et \( |1\rangle \).

Exemple :

\( |\psi\rangle \) = $\alpha$ \( |0\rangle \) + $\beta$ \( |1\rangle \)

où $\alpha$ et $\beta$ représentent les amplitudes associées à chaque état.

Les Portes quantiques

Les portes quantiques permettent de manipuler l'état des qubits dans un circuit quantique.

La porte Hadamard (H)

En informatique quantique, une porte quantique est l'équivalent d'une porte logique classique, mais appliquée à des qubits. Parmi les plus importantes, la porte Hadamard (H) joue un rôle central :
elle sert à créer une superposition équiprobable à partir d'un état de base.

1. Intuition

• Un bit classique est soit 0, soit 1.
• Un qubit, avant la mesure, peut être dans une combinaison de \( |0\rangle \) et \( |1\rangle \).
• La porte Hadamard transforme un état de base en superposition où les deux résultats sont possibles avec la même probabilité.

2. Forme mathématique

En notation matricielle, la porte Hadamard est définie par : $$H = \frac{1}{\sqrt{2}} \begin{pmatrix}1 & 1\\1 & -1\end{pmatrix}$$

3. Calculs

Cas \( |0\rangle \)

$$ |0\rangle = \begin{pmatrix}1 \\0 \end{pmatrix} $$

Application de H :

$$H |0\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix}1 & 1\\1 & -1\end{pmatrix}\begin{pmatrix}1 \\0 \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix}1 \\1 \end{pmatrix}$$

Ce qui donne :

$$H |0\rangle = \frac{ \ |0\rangle + |1\rangle}{\sqrt{2}} $$

Cas \( |1\rangle \)

$$ |1\rangle = \begin{pmatrix}0 \\1 \end{pmatrix} $$

Application de H :

$$H |1\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix}1 & 1\\1 & -1\end{pmatrix}\begin{pmatrix}0 \\1 \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix}1 \\-1 \end{pmatrix}$$

Ce qui donne :

$$H |1\rangle = \frac{ \ |0\rangle - |1\rangle}{\sqrt{2}} $$

La porte Hadamard est un outil pour préparer le terrain avant d'appliquer d'autres portes (comme CNOT) afin de créer des états intriqués ou de tester simultanément plusieurs cas dans un algorithme.

Circuit 1 : Circuit simple avec 1 qubit (sans mesure).

Dans ce premier circuit quantique, nous utilisons un seul qubit. En lui appliquant une porte Hadamard (H), on le place dans un état de superposition : il est à la fois dans l'état \( |0\rangle \) et \(|1\rangle \). Aucune mesure n'est effectuée.

                    from qiskit import QuantumCircuit
                    from qiskit.visualization import circuit_drawer
                    import matplotlib.pyplot as plt

                    # Circuit : 1 qubit
                    qc = QuantumCircuit(1)

                    # Application d'une porte Hadamard
                    qc.h(0)

                    # Affichage du circuit
                    print(qc.draw())
                    plt.show()
                

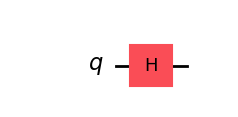
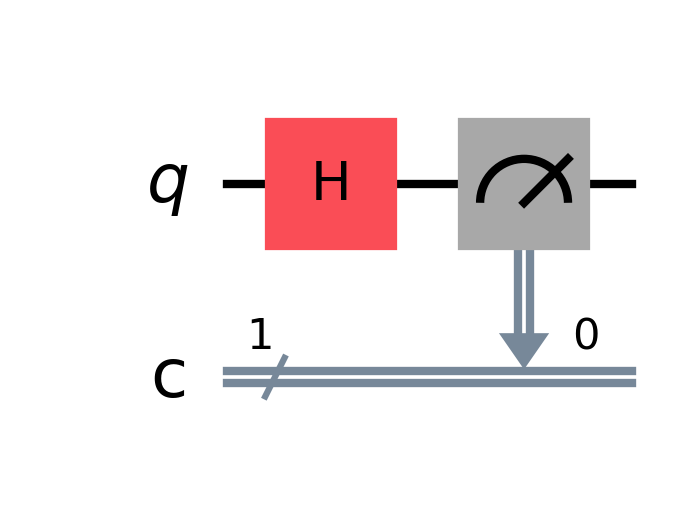
Circuit 2 : Circuit avec un qubit, un bit classique et une mesure.

Ce circuit quantique utilise une porte Hadamard (H) à un qubit initialisé à \( |0\rangle \), le mettant en superposition entre \( |0\rangle \) et \( |1\rangle \). Lors de la mesure (effectuée 1000 fois), on obtient environ 50 % de 0 et 50 % de 1, comme le montre l'exemple de résultat suivant : {'1': 498, '0': 502}.

Ce petit exemple montre l'un des principes fondamentaux du calcul quantique :

la nature probabiliste des mesures quantiques.

                    from qiskit import QuantumCircuit, transpile
                    from qiskit_aer import AerSimulator
                    from qiskit.visualization import plot_histogram
                    import matplotlib.pyplot as plt

                    # Création d'un circuit avec 1 qubit et 1 bit classique
                    qc = QuantumCircuit(1, 1)

                    # Porte Hadamard : crée une superposition sur le qubit 0
                    qc.h(0)
                    qc.measure(0, 0)  # Mesure du qubit 0
                    print(qc.draw())  # Affichage du circuit dans la console

                    # Initialisation du simulateur
                    simulator = AerSimulator()

                    # Exécution du circuit
                    compiled_circuit = transpile(qc, simulator)
                    simu = simulator.run(compiled_circuit, shots=1000)
                    result = simu.result()

                    # Récupérer les résultats
                    counts = result.get_counts()
                    print("Résultats de la mesure :", counts)

                    # Affichage des résultats
                    
                    plot_histogram(counts)
                    plt.show()

                    
                

                    # Création d'un circuit avec 2 qubits et 2 bits classique
                    qc = QuantumCircuit(2, 2)

                    # Porte Hadamard sur le premier qubit
                    qc.h(0)

                    # Porte CNOT (intrication)
                    qc.cx(0, 1)
                    qc.measure([0, 1], [0, 1])  # Mesure des deux qubits

                    # Affichage du circuit
                    print(qc.draw())

                    # Initialisation du simulateur
                    simulator = AerSimulator()

                    # Exécuter le circuit pour le simulateur
                    compiled_circuit = transpile(qc, simulator)
                    simu = simulator.run(compiled_circuit, shots=1000)
                    result = simu.result()

                    # Récupérer les résultats
                    counts = result.get_counts()
                    print("Résultats de la mesure :", counts)

                    ...
                    
                    Résultats de la mesure : {'00': 502, '11': 498}

                    
                

                        from qiskit import QuantumCircuit
                        qc = QuantumCircuit(2, 1)

                        # Préparation
                        qc.h(0)
                        qc.x(1)
                        qc.h(1)

                        # Oracle (boîte noire)
                        qc.cx(0, 1)

                        # Lecture
                        qc.h(0)
                        qc.measure(0, 0)

                        qc.draw('mpl')
                        
                    

Pour illustrer l'algorithme de Deutsch-Jozsa, on peut représenter deux circuits différents selon la nature de l'oracle (la "boîte noire" qui encode la fonction).
Dans le premier cas, l'oracle est constant et le résultat de la mesure est toujours 0.
Dans le second cas, l'oracle est équilibré et la mesure retourne toujours 1.
Ces circuits montrent comment un calcul quantique permet de déterminer, en une seule évaluation de l'oracle, si la fonction est constante ou équilibrée, alors qu'en informatique classique il faudrait plusieurs évaluations.

Cas 1 - Fonction constante

Le circuit associé produit toujours la sortie 0 :

Résultat circuit constant : {'0': 1024}

                    backend = Aer.get_backend('qasm_simulator')
                    qc_constant = QuantumCircuit(2, 1)
                    qc_constant.x(1)  # Préparation du second qubit en |1>
                    qc_constant.h([0, 1])

                    # Oracle constant : la fonction renvoie toujours la même valeur
                    qc_constant.h(0)
                    qc_constant.measure(0, 0)

                    # Transpile et exécution
                    tqc_constant = transpile(qc_constant, backend)
                    job_constant = backend.run(tqc_constant, shots=1024)
                    counts_constant = job_constant.result().get_counts()

                    print("Résultat circuit constant :", counts_constant)
                    qc_constant.draw('mpl')
                    plot_histogram(counts_constant)
                    
                

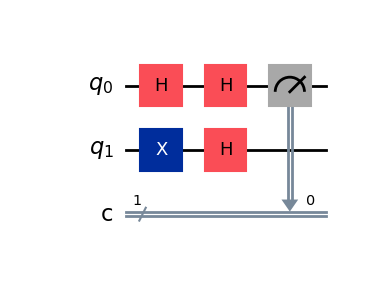
Cas 2 - Fonction équilibrée

Le circuit associé produit toujours la sortie 1 :

Résultat circuit équilibré : {'1': 1024}

                    backend = Aer.get_backend('qasm_simulator')

                    qc_balanced = QuantumCircuit(2, 1)
                    qc_balanced.x(1)  # Préparation du second qubit en |1>
                    qc_balanced.h([0, 1])
                    qc_balanced.cx(0, 1)  # Oracle équilibré
                    qc_balanced.h(0)
                    qc_balanced.measure(0, 0)

                    # Transpile et exécution
                    tqc_balanced = transpile(qc_balanced, backend)
                    job_balanced = backend.run(tqc_balanced, shots=1024)
                    counts_balanced = job_balanced.result().get_counts()

                    print("Résultat circuit équilibré :", counts_balanced)
                    qc_balanced.draw('mpl')
                    plot_histogram(counts_balanced)
                    
                

Interprétation du résultat

Dans l'algorithme de Deutsch-Jozsa, la mesure du premier qubit permet de déterminer immédiatement la nature de la fonction :

• Résultat 0 -> fonction constante
• Résultat 1 -> fonction équilibrée