Modélisation et visualisation du système de Lorenz

Décembre 2025

I. Aux frontières du chaos : le système de Lorenz

1. De la divergence au chaos - Explorer un système sensible

Imaginons deux trajectoires presque identiques : Elles commencent à peine séparée d'une quantité minuscule qu'on appelle $ \varepsilon $. Dans un système stable, cette petite différence reste négligeable au fil du temps. Mais dans un système sensible aux conditions initiales, comme ceux que l'on trouve par exemple en météorologie ou en dynamique des fluides, cet écart initial se met à croître exponentiellement :

$ d(t) = \varepsilon ~e^{\lambda t} $

où $ \lambda $ représente l'exposant de Lyapunov. Celui-ci mesure la vitesse à laquelle deux trajectoires s'éloignent :

si $ \lambda $ > 0, le système est dit chaotique.

Cette idée qui paraît simple, est au cœur du chaos déterministe : même dans un système gouverné par des lois parfaitement prévisibles, une minuscule variation dans les conditions initiales rend toute prévision à long terme impossible. La figure ci-dessous illustre un exemple de la divergence exponentielle : deux trajectoires, d'abord confondues, finissent par s'écarter rapidement au fil du temps.

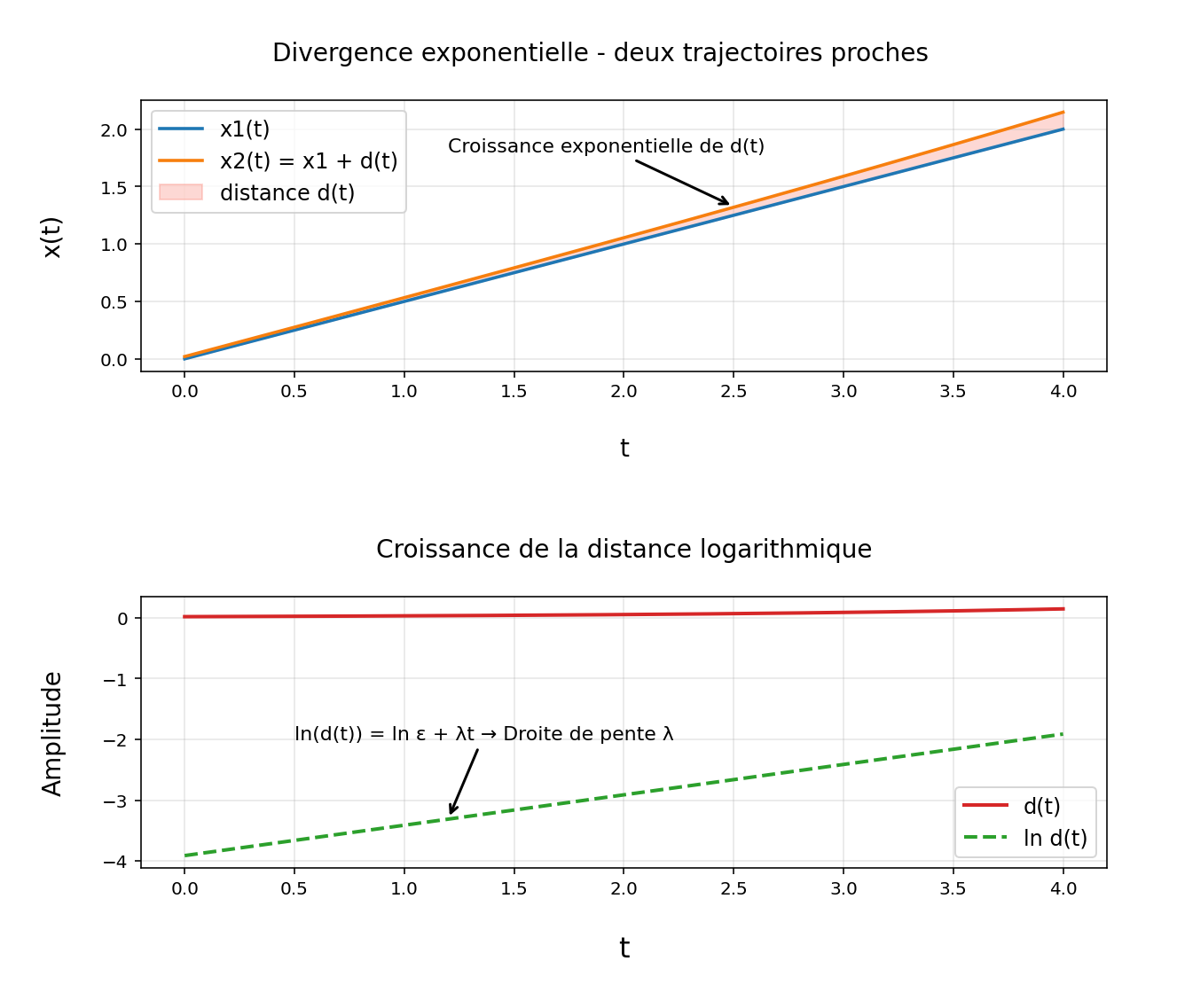
Figure 1 - Divergence exponentielle de deux trajectoires proches : la distance $ d(t) $ croît selon une loi $ \varepsilon~e^{\lambda t} $
entre deux trajectoires x₁(t) et x₂(t).

Considérons deux particules dont les positions au cours du temps sont notées x₁(t) et x₂(t). Si la seconde commencent très légèrement décalée de la première, à une distance initiale $ \varepsilon $ = 0.02, on a : d(t) = |x₂(t) - x₁(t)|.

Si le système est stable, la distance d(t) reste presque constante. Les deux trajectoires évoluent parallèlement.
En revanche, dans un système sensible aux conditions initiales, cette distance croît au fil du temps selon une loi exponentielle : $ d(t) = \varepsilon ~ e^{\lambda t} $. Ici, $ \lambda $ est l'exposant de Lyapunov, qui mesure la vitesse de divergence entre les deux trajectoires. Plus $\lambda$ est grand, plus les trajectoires s'éloignent rapidement. C'est la signature d'un comportement chaotique.

La notion de divergence exponentielle permet de comprendre comment un système apparemment simple peut devenir imprévisible. Pour illustrer ce phénomène de manière concrète, je me suis intéressée à un modèle emblématique passionnant : le système de Lorenz. Développé en 1963 par le météorologue Edward Lorenz, ce système d'équations différentielles cherchait initialement à modéliser la convection de l'air atmosphérique. Pourtant, il révéla plus que cela : une sensibilité extrême aux conditions initiales, conduisant à un comportement chaotique, même si les équations sont parfaitement déterministes.
On va maintenant voir comment il se définit et comment ses trajectoires évoluent dans le temps.

2. Les équations du modèle : un système simple, une dynamique imprévisible

Le système de Lorenz est un ensemble de trois équations différentielles couplées non linéaires décrivant l'évolution simplifiée d'un fluide chauffé par le bas et refroidi par le haut. Les trois variables x(t), y(t) et z(t) représentent respectivement le mouvement du fluide (vitesse de la convection), la différence de température entre deux points du fluide, et la variation de la température verticale par rapport à l'équilibre :

$$ \begin{cases} \dfrac{dx}{dt} = \sigma [y(t) - x(t)] \\[6pt] \dfrac{dy}{dt} = x(t)[\rho - z(t)] - y(t) \\[6pt] \dfrac{dz}{dt} = x(t)y(t) - \beta z(t) \end{cases} $$

avec trois paramètres fixés :

$\sigma$ : le nombre de Prandtl, lié à la viscosité du fluide,
$\rho$ : le nombre de Rayleigh réduit, qui détermine la différence de température entre le bas et le haut du système,
$\beta$ : un coefficient géométrique associé à la forme du système de convection.

Quand on résout ces équations pour différentes valeurs de ($\sigma$, $\rho$, $\beta$), on découvre des comportements radicalement différents :

Pour certaines valeurs, le système se stabilise (équilibre).
Pour d'autres, il oscille régulièrement (périodique).
Et pour un ensemble de paramètres bien précis, il devient chaotique, c'est à dire :

sensible à la moindre variation initiale,
impossible à prédire à long terme,
mais confinée dans une structure ordonnée: l'attracteur de Lorenz, une forme de papillon 🦋.

3. A quoi ressemble le Lorenz ? Première visualisation de l'attracteur

Ci-dessous, je montre trois attracteurs de Lorenz correspondant à différents ensembles de paramètres. On y observe trois comportements distincts : stable, périodique et chaotique.

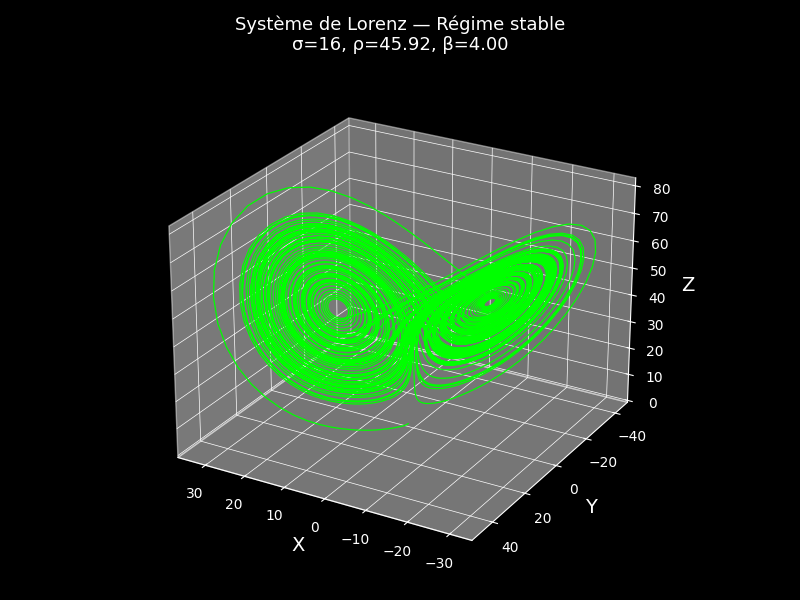
Figure 2 - Régime stable

Les trajectoires du régime stable convergent rapidement vers un petit cycle central. Le système revient toujours vers le même état, même après une petite perturbation. Le cercle central apparaît dense car toutes les trajectoires se rassemblent.

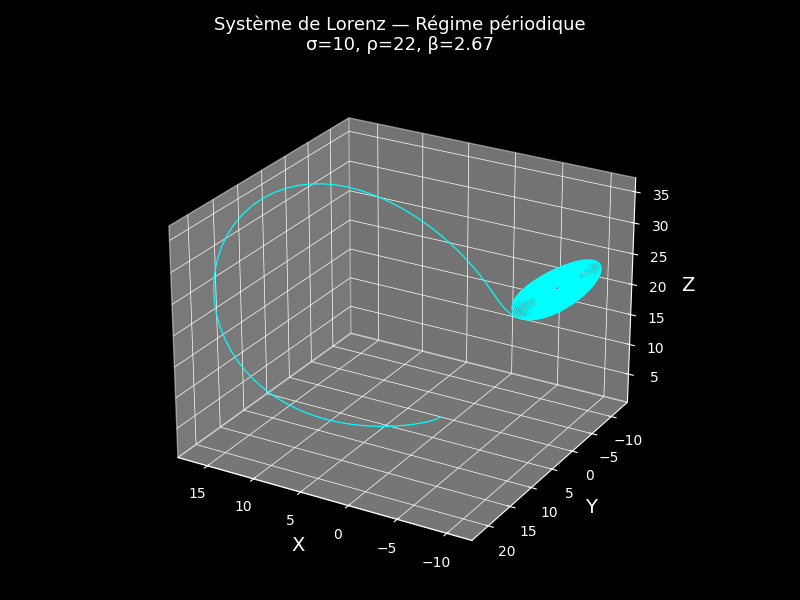
Figure 3 - Régime Périodique

Le système d'un régime périodique suit un cycle régulier et répétitif. La trajectoire forme une boucle ou un ovale fermé qui se répète dans le temps. La dynamique reste prévisible et ne diverge pas.

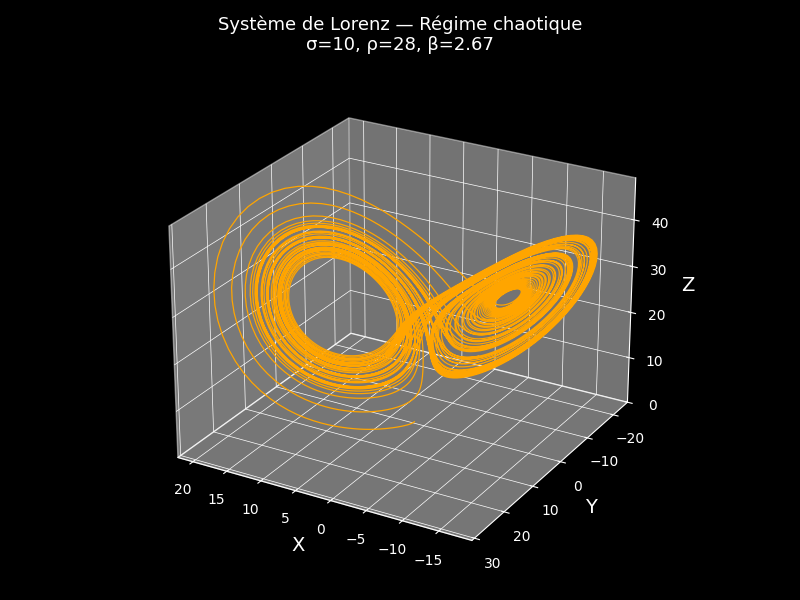
Figure 4 - Régime Chaotique

Le célèbre papillon de Lorenz. Ici, de petites différences initiales entrainent des divergences rapides . Les deux ailes du papillon montrent comment les trajectoires s'étendent sur tout l'espace disponible. Le centre reste moins dense, illustrant la sensibilité extrême aux conditions initiales. L'extrait de code ci-dessous montre la simulation du régime chaotique du système de Lorenz. On observe la forme caractéristique en papillon : deux zones d'attraction entre lesquelles la trajectoire alterne de manière imprévisible. Ce comportement illustre la sensibilité aux conditions initiales, signature du chaos déterministe.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# --- Système de Lorenz ---
def lorenz(t, state, sigma=10.0, rho=28.0, beta=8/3):
    x, y, z = state
    dx = sigma * (y - x)
    dy = x * (rho - z) - y
    dz = x * y - beta * z
    return [dx, dy, dz]

# --- Paramètres chaotiques ---
sigma, rho, beta = 10, 28, 8/3
y0 = [1.0, 1.0, 1.0]
t_span = (0, 70)
t_eval = np.linspace(0, 70, 15000)

# --- Résolution numérique ---
sol = solve_ivp(lorenz, t_span, y0, t_eval=t_eval, args=(sigma, rho, beta))
x, y, z = sol.y

# --- Tracé du papillon ---
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z, color='orange', lw=0.6)

ax.set_title("Régime chaotique du système de Lorenz", fontsize=14, pad=10)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")

# Grille douce et claire
for axis in [ax.xaxis, ax.yaxis, ax.zaxis]:
    axis._axinfo["grid"].update({"color": (1, 1, 1, 0.15), "linestyle": ":", "linewidth": 0.5})

plt.tight_layout()
plt.show()

Comme on peut le voir dans le tableau ci-dessous, Les valeurs des paramètres du système de Lorenz influencent fortement le comportement des trajectoires. Pour des valeurs faibles de $\rho$, le système converge vers un point stable ; pour $\rho$ = 28, il devient chaotique ; au-delà, les trajectoires divergent rapidement.

Cas	σ (sigma)	ρ (rho)	β (beta)	Comportement
1	16	45,92	4	Stable
2	10	28	8/3	Chaotique
3	10	22	8/3	Périodique

Tableau 1 - comportement en fonction des paramètres

II. L'aile du papillon : sensibilité extrême aux conditions initiales

Une des caractéristiques les plus fascinantes du système de Lorenz est sa sensibilité extrême aux conditions initiales. Deux trajectoires qui partent d'états presque identiques vont, au début, rester proches l'une de l'autre, mais au fil du temps, elles s'éloignent rapidement. Ce phénomène que l'on appelle divergence exponentielle, est le signe distinctif du chaos déterministe: le système obéit à des lois simples, mais son évolution devient imprévisible à long terme.

La figure ci-dessous montre comment la distance entre deux trajectoires évolue au cours du temps. Au début, la différence infinitésimale ($ \varepsilon \approx 10^{-8} $), mais la courbe montre qu'elle croît de manière exponentielle avant de se stabiliser autour d'une valeur moyenne : les deux trajectoires finissent par explorer des zones complètement différentes de l'espace des phases.

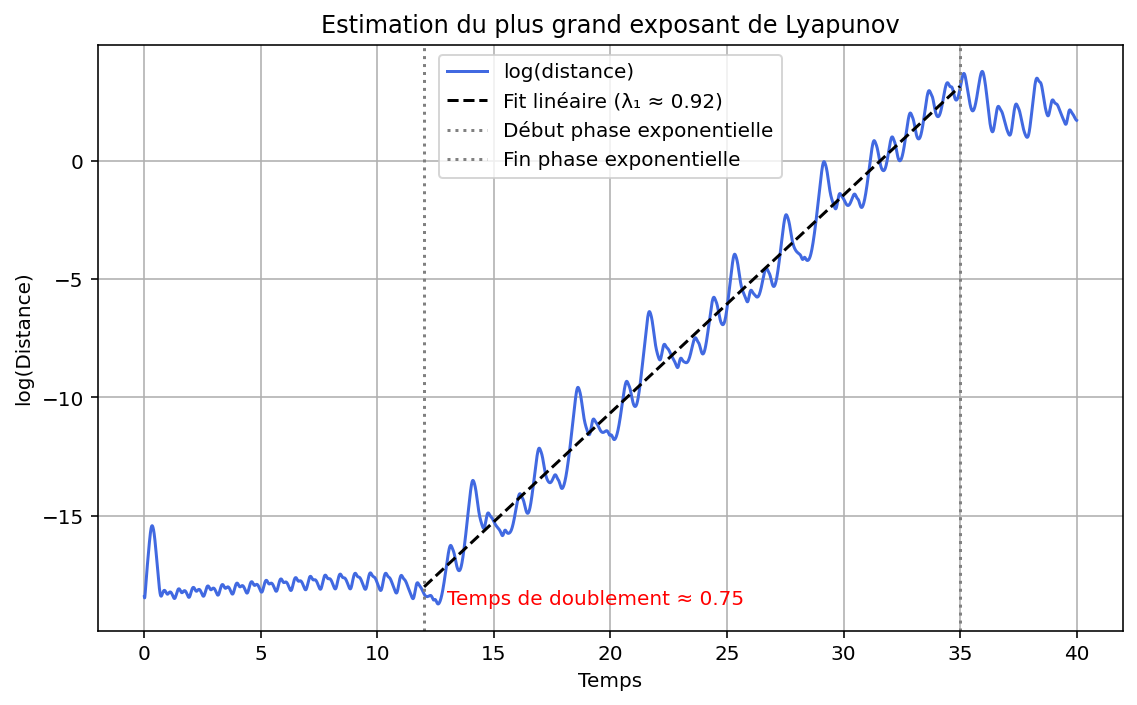
Figure 5 - Le graphique montre la courbe log(distance) entre les deux trajectoires, la zone linéaire utilisée pour la régression (entre t=12 et t=35), la droite de régression représentant la croissance exponentielle et le temps de doublement des erreurs annoté directement sur la figure.

La pente initiale de cette courbe est liée à ce que l'on appelle l'exposant de Lyapunov ($ \lambda $), une grandeur qui mesure la vitesse moyenne de divergence des trajectoires voisines. Un exposant positif signifie que les trajectoires s'écartent exponentiellement dans le temps. C'est le cas du régime chaotique du système de Lorenz.

En revanche, dans un régime stable ou périodique, cette distance reste bornée ou revient à zero : les trajectoires restent proches ou reviennent sur elles-mêmes.

Pour le système de Lorenz classique ($ \sigma = 10, \rho = 28, \beta = 8/3 $), on sait que le système est chaotique.

Une façon de quantifier cette sensibilité aux conditions initiales est de calculer le plus grand exposant de Lyapunov ($ \lambda_1 $), qui mesure le taux de divergence exponentielle de trajectoires initialement proches :

$ \Delta (t) \sim \Delta_0 e^{\lambda_1 t} $

où $ \Delta (t) $ est la distance entre deux trajectoires et $ \Delta_0 $ la perturbation initiale.

1. Méthode : comparer deux trajectoires presque identiques

Nous avons simulé deux trajectoires initialement très proches, avec une différence $ \Delta_0 = 10^{-8} $.
L'intégration a été réalisé avec solve_ivp en utilisant une méthode de haute précision (DOP853) et des tolérances strictes (rtol=1e-10, atol=1e-12) pour éviter que les erreurs numériques n'influencent la croissance initiale.
La distance $ \Delta (t) $ entre les deux trajectoires a été calculée en norme euclidienne.
La phase exponentielle a été identifiée sur le graphe de $ log(\Delta (t)) $ comme la portion linéaire de la courbe. Pour notre simulation, cette phase se situe entre t $ \approx 12 $ et $ t \approx 35 $.

2. Résultats : une divergence exponentielle

Une régression linéaire sur $ log(\Delta (t)) $ dans cette fenêtre a donné :

$ {\lambda_1} \approx 0,92 $

Cette valeur est positive, confirmant la nature chaotique du système de Lorenz.
Le temps de doublement des erreurs, c'est à dire le temps nécessaire pour que deux trajectoires initialement proches doublent leur séparation, est donné par :

$ t_{double} = \dfrac{ln 2}{\lambda_1} \approx 0,75 $

3. Interprétation : la signature du chaos

La valeur $ \lambda_1 \approx 0,92 $ signifie qu'une petite erreur initiale double toutes les $\sim$ 0,75 unités de temps.
Après $ t \approx 35 $, la distance entre trajectoires se sature à l'échelle de l'attracteur, et la croissance exponentielle n'est plus observable.
Cette analyse illustre de façon quantitative la sensibilité aux conditions initiales, caractéristique des systèmes chaotiques comme le Lorenz.

III. Anatomie d'un attracteur étrange : étude dynamique du système

1. Paramètres du modèle : $ \sigma, \rho, \beta $ et leur rôle dans la dynamique

Dans cette section, nous analysons en profondeur la dynamique du système de Lorenz défini par :

$$ \begin{cases} \dot{x} = \sigma (y - x) \\[6pt] \dot{y} = x (\rho - z) - y \qquad \sigma = 10, ~\rho = 28, ~\beta = 8/3\\[6pt] \dot{z} = xy - \beta z \end{cases} $$

Ces paramètres correspondent au régime chaotique classique, dans lequel le système possède un attracteur étrange. Pour analyser sa dynamique, nous intégrons numériquement les équations différentielles avec une précision élevée.

2. Simuler la trajectoire : résoudre numériquement les équations de Lorenz

L'extrait de code ci-dessous est utilisé pour définir et intégrer le système :

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# ---------- Paramètres ----------
sigma, rho, beta = 10.0, 28.0, 8/3

# ---------- Système de Lorenz ----------
def lorenz(t, state):
    x, y, z = state
    return [sigma*(y-x), x*(rho-z)-y, x*y - beta*z]

# ---------- Simulation (longue) ----------
x0 = [1.0, 1.0, 1.0]

sol = solve_ivp(lorenz, (t0, tf), x0, t_eval=t_eval, method='DOP853',
                rtol=1e-10, atol=1e-12)
X = sol.y.T 
t = sol.t

Le solveur est de haute précision car :

le système est fortement chaotique, donc sensible aux erreurs numériques,
une mauvaise tolérance peut contaminer les trajectoires,
le calcul des éléments nécessite une grande stabilité.

3. Plonger dans l'espace d'état : attracteur 3D et projections 2D

La trajectoire tridimensionnelle obtenue après élimination des transitoires (t >10).

mask = t > 10.0
X_ss = X[mask]
t_ss = t[mask]

Le graphique ci-dessous montre la structure en double lobe, typique du Lorenz. Cette structure est un attracteur étrange.

La figure montre :

La trajectoire est confinée dans un ensemble compact.
Elle ne se ferme jamais sur elle-même, absence de périodicité..
La structure est fractale : des motifs similaires apparaissent à différente échelles.
La trajectoire passe continuellement d'une aile à l'autre, de manière chaotique.

L'attracteur étrange est la signature géométrique du chaos.

Les projections 2D permettent de mieux comprendre la géométrie interne de l'attracteur. Elles révèlent :

La projection $ (x, y) $ montre deux spirales imbriquées.
La projection $ (x, z) $ met en évidence les lobes verticaux de l'attracteur.

Conclusion : les projections révèlent les régions où la dynamique est compressée ou étirée.

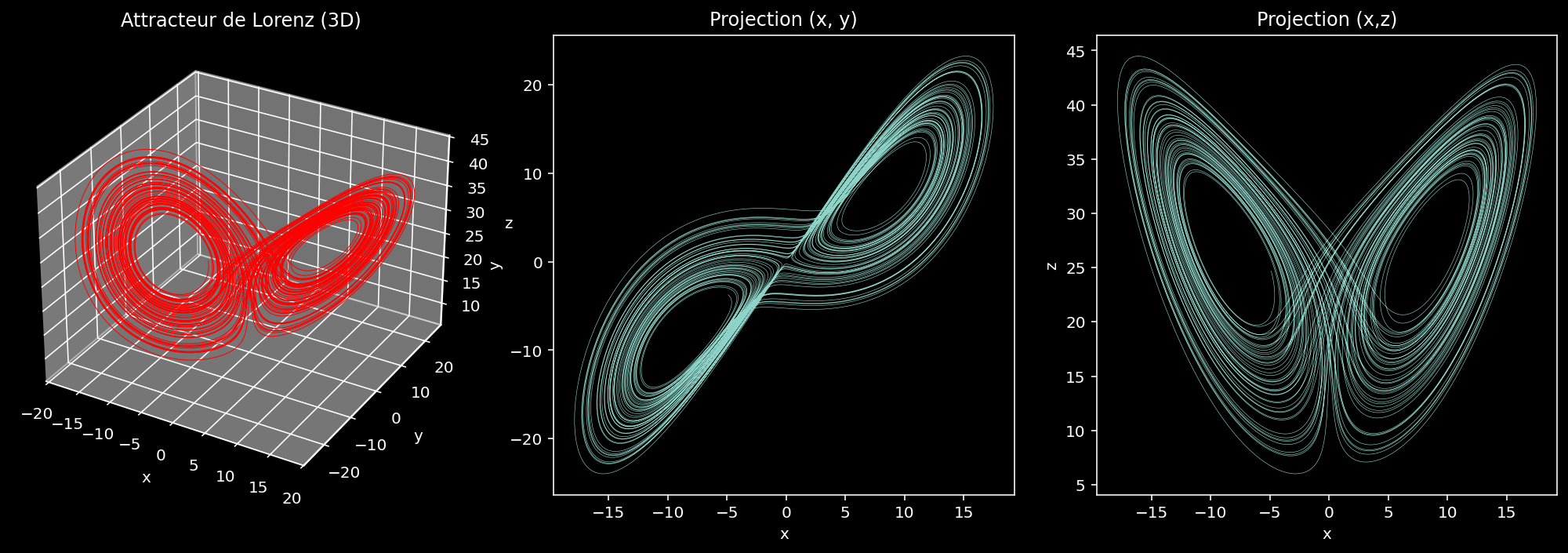
Figure 6 - Projections 2D $ \ (x, y) \ $ et $ \ (x, z) \ $ .

4. Découper le chaos : la section de Poincaré

La section de Poincaré est un outil fondamental en dynamique non linéaire. Elle permet de réduire une trajectoire continue dans l'espace des phases (ici 3D) à un ensemble de points dans un plan (2D), ce qui simplifie l'analyse tout en conservant les propriétés essentielles de la dynamique.
Pour le système de Lorenz, cette section montre de manière frappante la structure fractale de l'attracteur.

On fixe un plan dans l'espace d'état, par exemple : $ z = z_0 = 25 $
Chaque fois que la trajectoire coupe ce plan, on enregistre la position ($ x_n, y_n $). Cette méthode transforme une trajectoire 3D en un nuage de points 2D.

Voici un extrait du code :

La section de Poincaré appliquée au système de Lorenz révèle de manière nette la nature de son attracteur étrange. Le nuage de points présente une structure organisée, non aléatoire, mais néanmoins non périodique. Cette représentation 2D permet d'observer directement la fractalité et la complexité interne de l'attracteur, caractéristiques d'une dynamique chaotique.

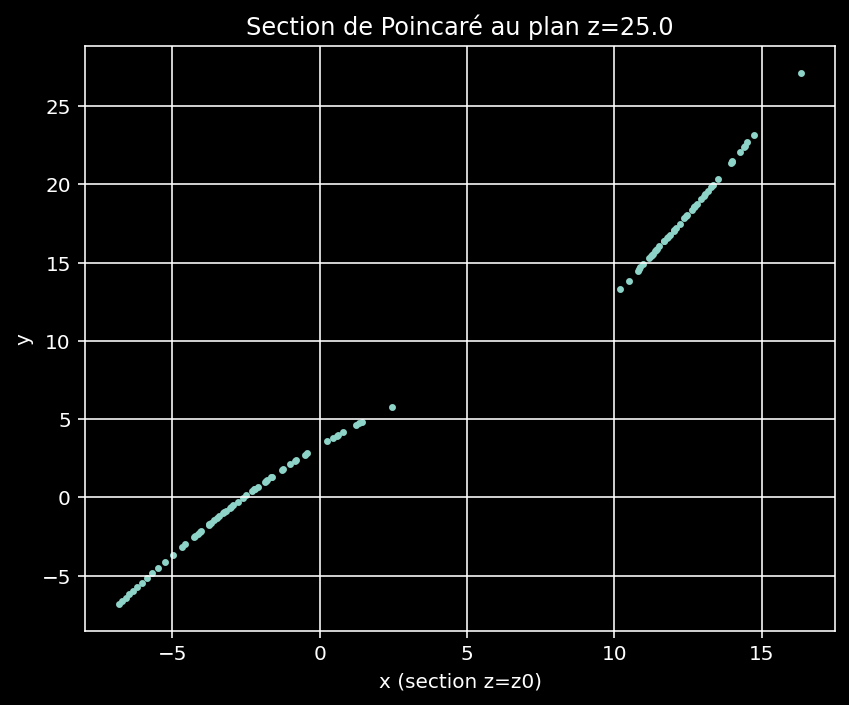
Figure 7 - Section de Poincaré.

5. La carte de retour (return map)

La carte de retour (figure ci-dessous) est un outil permettant d'étudier la dynamique d'un système chaotique en réduisant une trajectoire continue à une carte discrète. Elle consiste à prendre une suite d'événements précis (ici les maxima locaux de la variable $ x(t) $, puis à analyser la relation entre deux maxima successifs.

On commence par parcourir le signal $ x(t) $ pour identifier tous les points où $ x $ atteint un maximum. Un maximum local correspond à un point i où :

$ x_{i-1} < x_i \quad et \quad x_{i+1} < x_i $

Extrait de code :

# --- Carte de retour (Return Map) pour x(t) ---
x = sol.y[0]
t = sol.t

# Détection des maxima locaux
x_max = []
for i in range(1, len(x) - 1):
    if x[i-1] < x[i] and x[i+1] < x[i]:
        x_max.append(x[i])

# Transformation en tableaux numpy
x_max = np.array(x_max)

Ce tableau contient maintenant la suite : $ x_1, x_2, x_3,.. $ où chaque $ x_n $ est un maximum local de la composante $ x(t) $. Pour construire la carte de retour $ x_{n+1} = f(x_n) $, on associe à chaque maximum $ x_{n} $ le maximum suivant $ x_{n+1} $. On forme donc la suite de couples : $ (x_n, x_{n+1}) $

Dans le code :

# Points successifs : (x_n, x_{n+1})
x_n = x_max[:-1]  # tous sauf le dernier
x_np1 = x_max[1:]  # tous sauf le premier

Le tracé graphique permet de visualiser la relation discrète définie par le système :

plt.figure(figsize=(6, 6))
plt.scatter(x_n, x_np1, s=8)
plt.xlabel('$x_n$')
plt.ylabel('$x_{n+1}$')
plt.title('Carte de retour (Return Map) du système de Lorenz')
plt.grid(True, alpha=0.6)
plt.tight_layout()
plt.show()

La carte ne donne pas simplement un nuage de points aléatoire, ni une courbe unique. Le résultat observé possède plusieurs caractéristiques fondamentales :

1. Présence d'une structure continue mais irrégulière

Les points ne se regroupent pas en quelques valeurs précises : le système n'est pas périodique.
Ils ne se forment pas non plus un nuage totalement désordonné : la dynamique n'est pas aléatoire, elle est déterministe.

2. Forte sensibilité locale

La carte montre des zones où une très petite variation de $x_n$ produit une variation importante de $x_{n+1}$. Cela correspond aux régions où la dynamique du Lorenz est fortement étirée dans l'espace d'état. Ces régions sont responsables de :

la divergence rapide entre trajectoires,
l'imprévisibilité à long terme,
l'exposant de Lyapunov positif.

Conclusion : la carte de retour du système de Lorenz montre clairement que :

la dynamique n'est pas périodique,
elle n'est pas non plus aléatoire,
elle suit une loi déterministe complexe avec une structure fractale sous-jacente.

C'est un outil très efficace pour visualiser la nature chaotique mais déterministe du système.

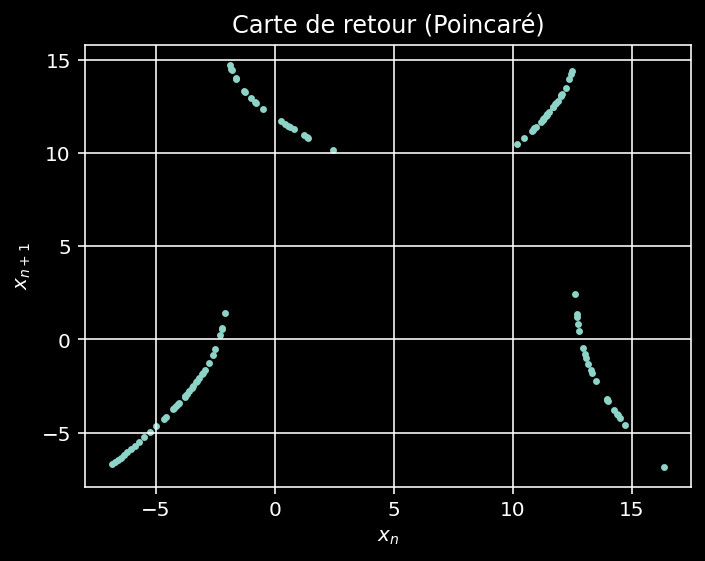
Figure 8 - Carte de retour (Poincaré).

6. Remonter le fil du temps : la série temporelle

La série temporelle est la représentation de l'évolution d'une variable du système (ici $ x(t) $) en fonction du temps. Elle constitue un premier indicateur essentiel pour identifier la nature de la dynamique : régulière, quasi-périodique ou chaotique.

Extrait du code :

# ---------- Série temporelle de x(t) ----------
plt.figure(figsize=(10, 5))
plt.plot(t_ss, X_ss[:, 0], lw=0.8)
plt.xlabel('Temps')
plt.ylabel('x(t)')
plt.title('Série temporelle (x)')
plt.grid(True)
plt.tight_layout()
plt.show()

L'allure de la série temporelle présente plusieurs caractéristiques typiques d'un système chaotique :

1. Une apparence oscillatoire mais non périodique.

La trajectoire oscille entre des valeurs positives et négatives, traduisant les passages successifs autour des deux lobes de l'attracteur. Cependant, contrairement à un signal périodique :

les maxima ne se répètent jamais exactement,
les durées entre pics varient,
le motif global ne revient jamais de manière identique.

Cela confirme l'absence de périodicité, propriété fondamentale du chaos.

2. Une alternance irrégulière entre les deux régimes dynamiques.

La série temporelle montre des séquences où la trajectoire reste longtemps dans un lobe, puis bascule soudainement vers l'autre. Ces transitions imprévisibles sont directement liées à la géométrie de l'attracteur et à la sensibilité aux conditions initiales.

3. Une dynamique confinée mais complexe.

Malgré son apparente "désorganisation", le signal n'explose pas et reste dans une plage bornée. Cela traduit le fait que ce comportement est caractéristique du Lorenz :

Le système est déterministe,
il évolue sur un attracteur étrange aux dimensions fractales.

4. Impact de la sensibilité aux conditions initiales.

Deux trajectoires très proches au départ donneraient deux séries temporelles qui se ressemblent au début, puis divergent rapidement. Cela se manifeste dans la série temporelle par :

des pics qui se désynchronisent,
des amplitudes qui se déphasent,
une perte progressive de corrélation.

La série temporelle met en évidence une dynamique oscillatoire mais non périodique, avec des transitions imprévisibles entre deux régimes. Elle constitue un premier indicateur clair du caractère chaotique du système de Lorenz en montrant à la fois la non périodicité, complexité et la sensibilité aux conditions initiales.

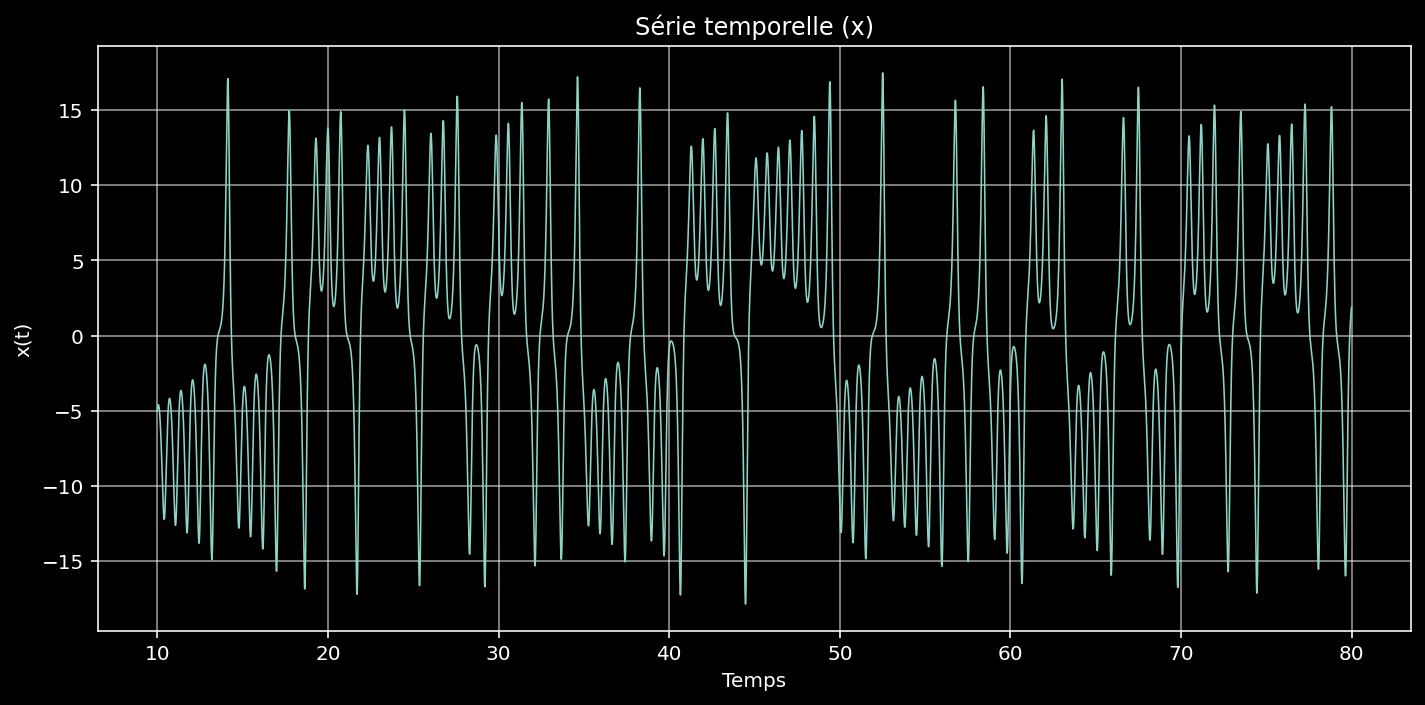
Figure 9 - Série temporelle.

7. Le chaos vu en fréquence : densité spectrale du signal

L'analyse spectrale permet d'étudier la répartition de l'énergie du signal dans le domaine fréquentiel. Pour un système chaotique, elle constitue un indicateur essentiel pour distinguer :

un comportement périodique (pics nets),
un comportement quasi-périodique (quelques pics multiples),
un comportement chaotique spectre large et irrégulier).

On applique cette analyse à la variable.

Extrait du code :

from scipy.signal import welch

fs = 1.0/dt  # fréquence d'échantillonnage
f, Pxx = welch(X_ss[:, 0], fs=fs, nperseg=4096)

plt.figure(figsize=(7, 4))
plt.semilogy(f, Pxx, color='purple')
plt.xlim(0, 5)  # zoom bas fréquences ; ajuste selon besoin
plt.xlabel('Fréquence (Hz)')
plt.ylabel('PSD')
plt.title('Densité spectrale de puissance (x)')
plt.grid(True, alpha=0.6)
plt.tight_layout()
plt.show()

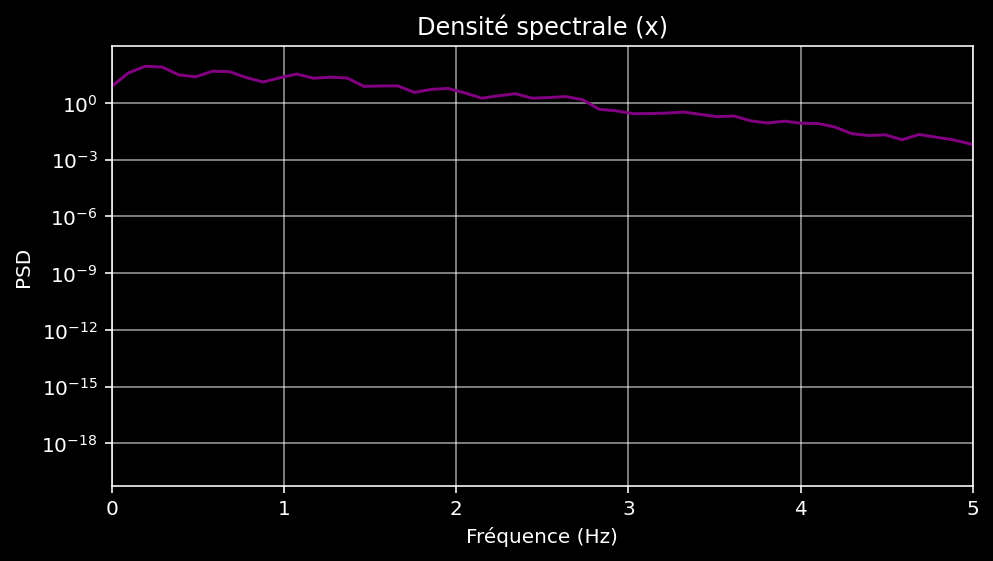
Figure 10 - Densité spectrale

La densité spectrale du système présente une structure typique d'un signal chaotique.

1. Absence de pics dominants nets

Contrairement à un système périodique (qui montre un pic très fin à une fréquence bien définie), le spectre :

ne présente pas de fréquence fondamentale forte,
montre des irrégularités sans périodicité évidente,
reflète l'absence de rythme répétitif dans le signal.

Cela confirme le caractère non périodique de la dynamique.

2. Un spectre continu et étalé (broadband spectrum)

Le spectre s'étale sur une large plage de fréquences. C'est la signature directe d'un système chaotique. L'énergie n'est pas concentrée sur quelques fréquences mais elle est répartie sur un ensemble large traduisant une dynamique riche et complexe. C'est un spectre large bande, opposé au spectre discret des systèmes réguliers.

3. Présence de petites structures internes

Même si le spectre est à large bande, on peut distinguer de petites bosses et des zones plus denses à certaines fréquences qui correspondent à des régularités statistiques locales

4. Correspondance avec la série temporelle

La série temporelle montrait déjà un comportement oscillatoire, irrégulier et sans répétition exacte. La densité spectrale est donc cohérente :
$\Rightarrow$ l'absence de période dans le domaine temporel se traduit en absence de pics nets dans le domaine fréquentiel.

8. Conclusion

La densité spectrale de puissance confirme clairement que la dynamique du système de Lorenz est chaotique : elle n'a pas de périodicité dominante, elle a un signal réparti sur un spectre large avec des fluctuations irrégulières et une absence de structure harmonique stable. Elle constitue un outil complémentaire aux sections précédentes pour identifier la nature chaotique du système.

Retour aux projets